NMR and Non-Square Jigsaw Puzzles
James Kitchens
August 17, 2020
Python
NMR
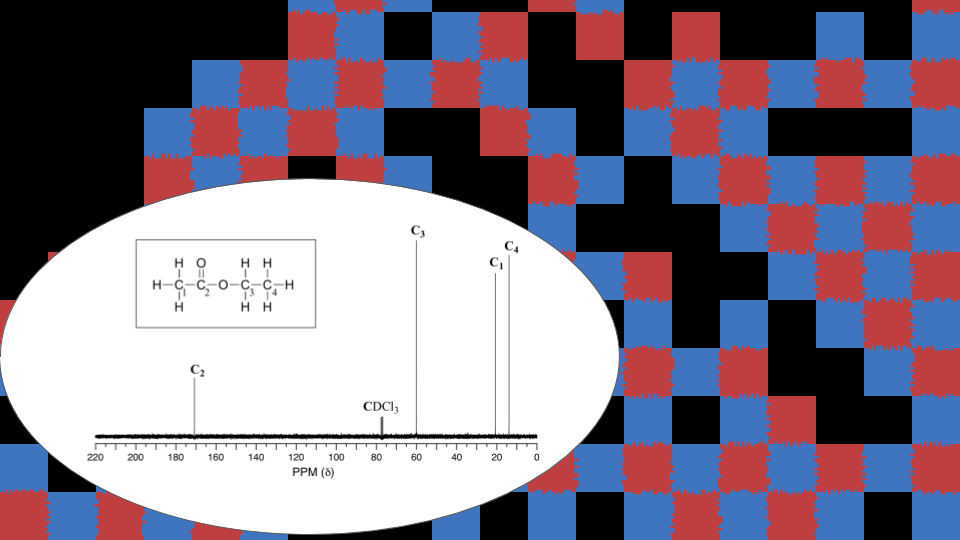
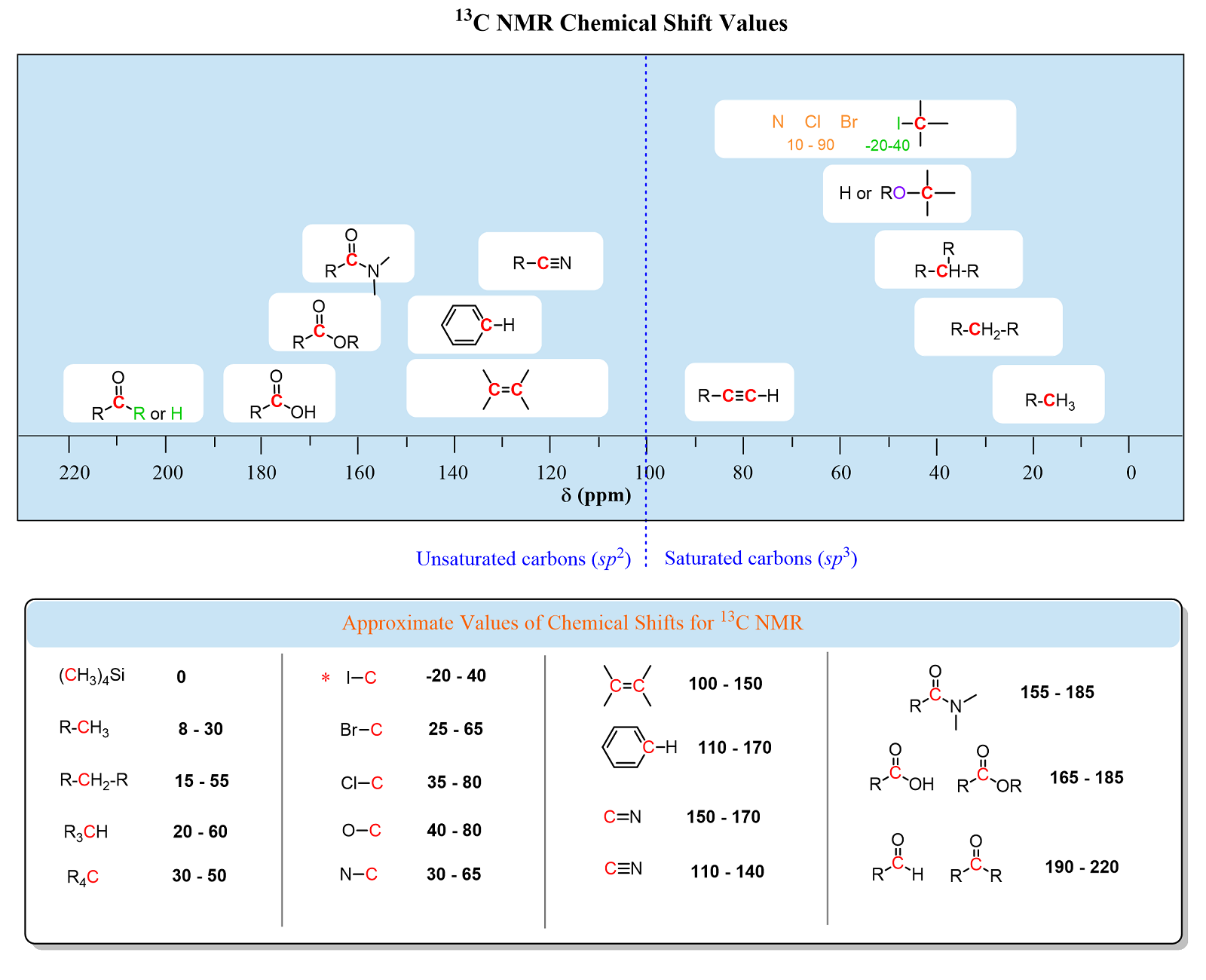
In organic chemistry during freshman year of undergraduate, we were discussing nuclear magnetic resonance (NMR) spectroscopy, a technique to determine the chemical structure of compounds in solution. Isotopes with an odd number of protons and/or neutrons, such as H-1 and C-13, have a resonant frequency within a spinning magnetic field that is dependent on the atoms that are bonded to them. Below is a map of these common resonant frequencies for C-13 NMR spectroscopy and their corresponding bonds:
In the laboratory, we worked through the structure of the compound bond by bond, piece by piece, identifying the unique way that functional groups were linked to illicit the spectra. Some spectra were obviously easier to determine than others, either due to the number of atoms or the complexity of the structure. I wondered if there was a method for automatically predicting the structure computationally based on the spectra alone, without the need for an underlying database of compounds and spectra.
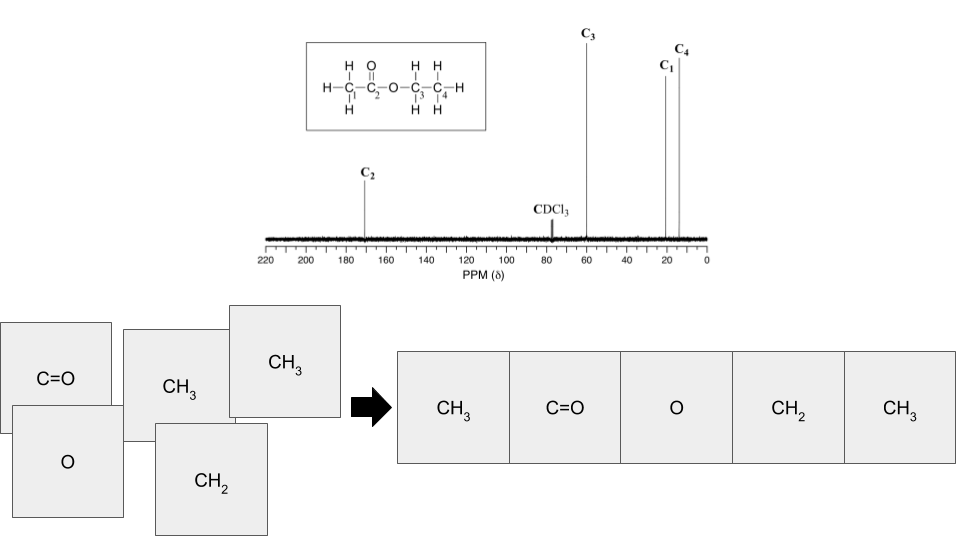
So, I began thinking about the compounds’ atoms or functional groups as pieces of a jigsaw puzzle with edges identifying the bonds known from the spectra. The puzzle, which would almost certainly have an irregular, non-square shape, would then be solved purely based on shape pieces’ edges. I thought about making this project my undergraduate senior thesis but instead decided to keep it as a fun creative side project. In this multipart blog post, I am going to walk you through my code and thought process behind the jigsaw puzzle creation, solving, and ultimately the future directions in which the concept could be expanded, especially with respect to the original goal of developing an NMR spectroscopy solver.
All of this code is written in Python and utilizes the PIL and random libraries. PIL stands for Python Image Library and is used for image creation and processing. The random library is within Python Standard Library, but PIL will have to be installed prior to working with this code.
Puzzle Creation
The puzzle consists of a grid of square puzzle pieces with jagged edges. The number of pieces and size of each piece set by the user. Each pixel along the piece’s edge has three possible states: -1, 0, or 1 (cavity, flat, or protrusion). I’ve forced the pixels closest to the corners of the piece to always be flat so that the pieces always visibly look contiguous.
creator.py
class JigsawPiece:
def __init__(self, size, empty = False, buildingConstraints = {}):
"""
Creates a square puzzle piece with jagged edges.
Pixels along edges have three states (-1-concave, 0-flat, 1-protrudes).
Corners are always flat to keep continuity
Parameters
size: integer, number of pixels in length/width of piece
empty: boolean, whether piece is empty or not
buildingConstraints: dictionary, any edge contraints from neighboring pieces
"""
self.empty = empty
self.pieceSize = size
self.pieceInfo = []
self.solvedOrientation = []
self.leftConstraints = {}
self.topConstraints = {}
self.rightConstraints = {}
self.bottomConstraints = {}
flatSide = [[],[],[],[]]
bumpList = [-1, 1]
if empty == True:
for info in range(size):
line = []
for element in range(size):
line.append("-")
self.pieceInfo.append(line)
else:
for info in range(size):
line = []
for element in range(size):
constrain = buildingConstraints.get(str(info) + "," + str(element), 3)
if constrain == 3:
if element != 1 and info != 1 and element != size - 2 and info != size - 2:
if info == 0 or info == size - 1:
if element != 0 and element != size - 1 and element != 1 and element != size - 2:
if element == size - 3:
if info == 0:
if 1 not in flatSide[0] and -1 not in flatSide[0]:
number = bumpList[random.randrange(2)]
else:
number = random.randrange(-1, 2)
else:
if 1 not in flatSide[2] and -1 not in flatSide[2]:
number = bumpList[random.randrange(2)]
else:
number = random.randrange(-1, 2)
else:
number = random.randrange(-1, 2)
line.append(number)
if info == 0:
flatSide[0].append(number)
else:
flatSide[2].append(number)
if info == 0:
self.topConstraints[str(size - 1 - info) + "," + str(element)] = 0 - number
else:
self.bottomConstraints[str(size - 1 - info) + "," + str(element)] = 0 - number
else:
line.append(0)
elif element == 0 or element == size - 1:
if info == size - 3:
if element == 0:
if 1 not in flatSide[3] and -1 not in flatSide[0]:
number = bumpList[random.randrange(2)]
else:
number = random.randrange(-1, 2)
else:
if 1 not in flatSide[1] and -1 not in flatSide[2]:
number = bumpList[random.randrange(2)]
else:
number = random.randrange(-1, 2)
else:
number = random.randrange(-1, 2)
line.append(number)
if element == 0:
flatSide[3].append(number)
else:
flatSide[1].append(number)
if element == 0:
self.leftConstraints[str(info) + "," + str(size - 1 - element)] = 0 - number
else:
self.rightConstraints[str(info) + "," + str(size - 1 - element)] = 0 - number
else:
line.append(0)
else:
line.append(0)
else:
line.append(constrain)
if info == 0:
self.topConstraints[str(size - 1 - info) + "," + str(element)] = 0 - constrain
elif info == size - 1:
self.bottomConstraints[str(size - 1 - info) + "," + str(element)] = 0 - constrain
elif element == 0:
self.leftConstraints[str(info) + "," + str(size - 1 - element)] = 0 - constrain
else:
self.rightConstraints[str(info) + "," + str(size - 1 - element)] = 0 - constrain
self.pieceInfo.append(line)
self.solvedOrientation = self.pieceInfo
In this version, I represented an edge without any connections as completely flat, similar to the edge pieces of a real 2D jigsaw puzzle. Each piece has a maximum of four connections and minimum of one connection. Lastly, I’ve given each piece the ability to rotate in 90 degree intervals. Pieces can be viewed as PNG images, with blue representing the piece shape.
creator.py
def rotatePiece(self):
"""
Rotates piece by 90 degrees clockwise, resets edge indices
"""
rotated = []
for row in range(self.pieceSize):
line = []
for column in range(self.pieceSize):
line.append(self.pieceInfo[self.pieceSize - 1 - column][row])
rotated.append(line)
self.pieceInfo = rotated
self.determineEdgeIndex()
def displayPiece(self, path):
"""
Saves single piece of puzzle as a png
Parameters
path: string, path to output png
"""
outFile = path
out = Image.new("RGB", (self.pieceSize + 2, self.pieceSize + 2))
for pixelLine in range(self.pieceSize + 2):
for pixel in range(self.pieceSize + 2):
out.putpixel((pixel, pixelLine), (255, 255, 255))
for pixelLine in range(self.pieceSize):
for pixel in range(self.pieceSize):
if self.pieceInfo[pixelLine][pixel] == -1:
out.putpixel((pixel + 1, pixelLine + 1), (255, 255, 255))
elif self.pieceInfo[pixelLine][pixel] == 1:
if pixel == 0:
out.putpixel((pixel, pixelLine + 1), (63, 116, 191))
elif pixel == self.pieceSize - 1:
out.putpixel((pixel + 2, pixelLine + 1), (63, 116, 191))
elif pixelLine == 0:
out.putpixel((pixel + 1, pixelLine), (63, 116, 191))
elif pixelLine == self.pieceSize - 1:
out.putpixel((pixel + 1, pixelLine + 2), (63, 116, 191))
out.putpixel((pixel + 1, pixelLine + 1), (63, 116, 191))
else:
out.putpixel((pixel + 1, pixelLine + 1), (63, 116, 191))
out.save(outFile)
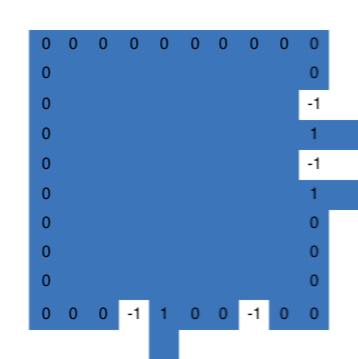
In order for pieces to fit together, they must have exact inverses of their edges; if Piece 1 has a “-1” at an edge pixel, then Piece 2 has to have a “1” at the corresponding opposite pixel. When building a neighboring piece to one that already exists, I added a building constraints parameter to ensure that the edge matches the neighboring piece’s edge. The program starts with a random piece on the puzzle grid and creates it without any edge building constraints, unless the piece is on the edge of the puzzle. From there, it builds the neighboring pieces, using the edge constraints from the original, working its way out until the entire grid is filled with pieces. This ensures that the entire puzzle will be continuous from every point on the puzzle; this is an important aspect when solving the puzzle. The entire puzzle can also be viewed as a PNG image, now with alternating colors (blue and red) to represent the different pieces. Once the puzzle is fully made, the program scrambles the order and rotation of all of the pieces, storing all of the pieces as an unordered list.
Solving
If I were solving a real 2D jigsaw puzzle, I would identify which pieces would work as edge pieces and try to build the outside frame of the puzzle. With the end goal that this method could be used to solve irregular, non-square shaped puzzles, identifying edge pieces would not always be an effective strategy.
creator.py
def determineEdgeIndex(self):
"""
Calculates edge indices by summing values along each edge, stored as list of integers
"""
self.edgeIndex = []
self.edges = [[], [], [], []]
if self.empty == True:
pass
else:
top = 0
bottom = 0
left = 0
right = 0
for row in range(len(self.pieceInfo)):
for column in range(len(self.pieceInfo[row])):
if row == 0:
top += self.pieceInfo[row][column]
self.edges[0].append(self.pieceInfo[row][column])
if row == self.pieceSize - 1:
bottom += self.pieceInfo[row][column]
self.edges[2].append(self.pieceInfo[row][column])
if column == 0:
left += self.pieceInfo[row][column]
self.edges[3].append(self.pieceInfo[row][column])
if column == self.pieceSize - 1:
right += self.pieceInfo[row][column]
self.edges[1].append(self.pieceInfo[row][column])
self.edgeIndex.append(top)
self.edgeIndex.append(right)
self.edgeIndex.append(bottom)
self.edgeIndex.append(left)
Instead, I calculated an edge index for each edge of each piece; this was done by summing the values of the pixels along the edge of the piece. I included this in the creator.py file as a method of the JigsawPiece class. Using this attribute of each edge, the program can more efficiently search through all of the potentially edge connections knowing that a compatible edge must have an edge index equal to the negative of the initial edge. This limits the search pool to only a few potential edges, rather than the entire list of scrambled pieces.
solver.py
def newSolvePuzzle(puzzle):
"""
Solves a scrambled puzzle that has pieces with all unique edges
Parameters
puzzle: puzzle, custom class (see creator.py Puzzle)
Return
dictionary, all pieces with unscrambled coordinates
"""
flatSide = [] # creates an example of a flat side for comparison, flat sides do not have connections
for number in range(puzzle.pieceSize): # loop based on piece size
flatSide.append(0)
pieceByLocation = {} # a dictionary containing the locations of every placed piece
startingPieceNotEmpty = False
increment = 0
while startingPieceNotEmpty == False:
if puzzle.scrambledPieces[increment].empty == False:
startingPieceNotEmpty = True
pieceByLocation[(0,0)] = puzzle.scrambledPieces[increment]
else:
increment += 1
previouslyUsedPieces = [] # a list of all previously placed pieces
previouslyUsedPieces.append(puzzle.scrambledPieces[0])
previouslyUsedCoordinates = [] # a list of all previously used coordinates, don't want to place two pieces on same coordinate
numberOfEmpties = 0
for emptyCheck in puzzle.scrambledPieces:
if emptyCheck.empty == True:
numberOfEmpties += 1
nonUniqueCoordinates = []
unplacedCoors = 0
while len(pieceByLocation) < (puzzle.puzzleSize**2)-numberOfEmpties-unplacedCoors:
coordinateCheck = False
while coordinateCheck == False: # this loop ensures that randomly selected coordinate is not used more than once
coordinateList = list(pieceByLocation.keys())
coordinate = coordinateList[random.randrange(0,len(coordinateList))]
if coordinate not in previouslyUsedCoordinates:
previouslyUsedCoordinates.append(coordinate)
coordinateCheck = True
piece = pieceByLocation[coordinate] # pulls piece from dictionary based on location
for edge in range(len(piece.edgeIndex)): # tries to match every edge of the piece
newPieceCoordinate = coordinateFromRelativeDirection(coord=coordinate, direction=edge)
if piece.edges[edge] == flatSide:
pass
elif newPieceCoordinate in list(pieceByLocation.keys()):
pass
else:
possibleConnectionsForEdge = []
for testPiece in puzzle.scrambledPieces:
if piece == testPiece: # cannot connect piece to itself, no reason to check
pass
elif testPiece.empty == True: # ignore empty pieces
pass
else:
for e in range(len(testPiece.edgeIndex)):
if testPiece in previouslyUsedPieces:
pass
elif piece.edgeIndex[edge] == -testPiece.edgeIndex[e]: # checks edge index before rotating
desiredEdge = (edge + 2) % 4 # uses index of edge in list to determine how to rotate
rotations = desiredEdge - e
if rotations < 0:
rotations = 4 + rotations
returnRotations = 4 - rotations
for rotate in range(rotations):
testPiece.rotatePiece()
check = edgeCheck(edge0=piece.edges[edge], edge1=testPiece.edges[desiredEdge])
if check == True: # if it passes the edge check, add to possible connections
possibleConnectionsForEdge.append(testPiece)
break
else:
for rotate in range(returnRotations):
testPiece.rotatePiece()
if len(possibleConnectionsForEdge) == 1: # setting up for possibility of non-unique edges in future
pieceByLocation[newPieceCoordinate] = possibleConnectionsForEdge[0]
previouslyUsedPieces.append(possibleConnectionsForEdge[0])
else:
return {}, False
unplacedCoors = 0
for nUCoor in nonUniqueCoordinates:
if nUCoor not in pieceByLocation:
unplacedCoors += 1
return pieceByLocation, True
Similar to how the puzzle was created, I thought it would best to start with a random piece and place. This piece is placed at (0, 0) with a fixed orientation and the program determines the coordinates of all other pieces relative to the starting piece. Subsequent pieces are rotated around to match edges with those already positioned. Once all of the pieces have been added, the coordinates of the puzzle as a whole are translated so that the top leftmost piece is given the coordinate (0, 0), an attribute of puzzles within the Puzzle class. The resulting puzzle may be in a different orientation than the original puzzle, but it will have all of the correct connections. It may also have a smaller size if the original puzzle was non-square and did not stretch all of the way to the edges of the canvas.

Expansions
In its current form, the program can solve non-square jigsaw puzzles composed of square shaped pieces that have at most four neighboring pieces. This is a pretty rigid restriction, which limits its application to a small subset of puzzles. For its purpose as an NMR spectroscopy solver, this may be a less impactful restriction as many times, scientists are working with carbon atoms that can make at most four bonds as well. For now, the most pressing issue is that all of the edges of the puzzle pieces must be unique and must match perfectly. This is directly counter to characteristics of NMR spectroscopy, where you may have multiple of the same atoms or functional groups and where you may not know all of the connections prior to attempting to solve.
All of the code used in this post can be found HERE. If you enjoyed this post and want to use this code yourself, give the repository a star on GitHub and fork the project to your own profile. If you have any questions, create an Issue for the GitHub repository and I will do my best to help!